—2025/06/06
ドメインずっと無料既に6月になって、今日の最高気温29度、熱い一日でした。
ブログの更新は2週間もしていなかった、今日はAtcoderの問題を解きたいと思います。
その前、ちょっと感動する話、
それでは、問題:
花壇に N 本の花が咲いており、それぞれ 1,2,……,Nと番号が振られています。最初、全ての花の高さは 0 です。 数列 h={h1,h2,h3,……} が入力として与えられます。以下の「水やり」操作を繰り返すことで、すべての k(1≦k≦N) に対して花 k の高さを h にしたいです。
- 整数 l,r を指定する。l≦x≦r を満たすすべての x に対して、花 x の高さを 1 高くする。
条件を満たすための最小の「水やり」操作の回数を求めてください。
なんか複雑そう、簡単に説明します。花壇にN本の花があって、最初一律高さは0、最終できにそれぞれの花の高さは与えられた数列のようになるため、水やりの最小回数を求めること。一回水やりすると、花の高さを1高くなる。
例を挙げて、見てみる。
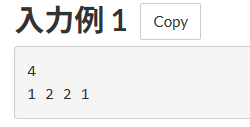
4本の花を最終的にそれぞれ 1, 2, 2, 1のように高くするため、水やりの最小回数を求める。
まず、最初の状態、

一回目水やりすると、

二回目水やりすると、


つまり、2回水やりすれば、4本の花はそれぞれ要求通りになります。
もう一例、

五本の花、最終的にそれぞれの高さは3,1,2,3,1になるため、水やりの最小回数を求める。
その流れは、
まず、

一回目水やり、

二回目水やり、

三回目水やり、

4回目水やり

五回目水やり
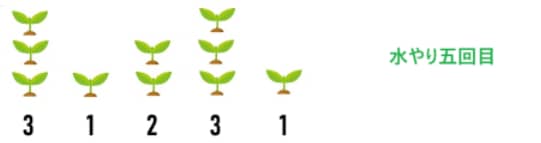
つまり、五回水やりをすると、それぞれの花の高さは与えられた数列のようになる。
ここまで2例の処理を纏める。
①花の高さは要求通りにならなければ、水やりを行う
②連続水やりの必要ある所まで一回水やりとして計上する、例えば、2例目の2回目の水やり、1本目花の最終高さは3、2本目花の最終高さは1,2本目花は1回だけ水やりすればよいので、2回目の水やりは一本目の花だけ。
以上はこの問題の解くための考え方ですが、java実装ためのアルゴリズムは何なんでしょう?
これはいわゆる典型的な再帰関数です。つまり、高さを逆にして考える。高さがあるもので隣り合っているものを連結しながら考えていく、この区間内のもの高さをそれぞれ – 1 ,全て0になるまでの回数を求める。
再帰関数はメリットとデメリットそれぞれあります、メリットはコードとしてはわかりやすくなりますが、再帰レベルが高くなると、メモリを使いすぎて、スタックオーバーフローになる。