—2025/04/21 動的計画法②——————-前編
今日のお天気は晴れ時々曇りです。
動的計画法について、前から気になって、なかなか上手に使えず、難しいアルゴリズムだと思います。
今回出遭った問題、動的計画法とそうじゃない方法を両方使って開発しました。
問題
英小文字からなる文字列 S が与えられます。 Tが空文字列である状態から始め、以下の操作を好きな回数繰り返すことで S=Tとすることができるか判定してください。
- T の末尾に
dreamdreamereraseeraserのいずれかを追加する。
例えば、
このような文字列S dreamerasererasedream
目視で判断すれば、答えがすぐ出ました。
dream + eraser + erase + dream
つまり、Tの4種類文字を使って、Sとピッタリの文字列を作れます。
でも、パソコンは人間ではないので、dream か dreamer か最初から2種類の選択が生じます。
コーディングする際、最初は普通の考え方を用いて、ソースを書きました。
①4種類の文字列を観察すれば、最長7桁のdreamer, 6桁のeraser、5桁のeraseとdream、桁数から着目します。
②読まれた文字の7桁目まではdreamerであれば、その後ろ続けられるのはase或はaser、処理が続く
③上記の状況に合わなければ、読まれた文字の6桁目まではeraserであれば、処理が続く
④上記の状況が合わなければ、読まれた文字の5桁目まではerase か又は dreamであれば、処理が続く
図で現わしてみる、
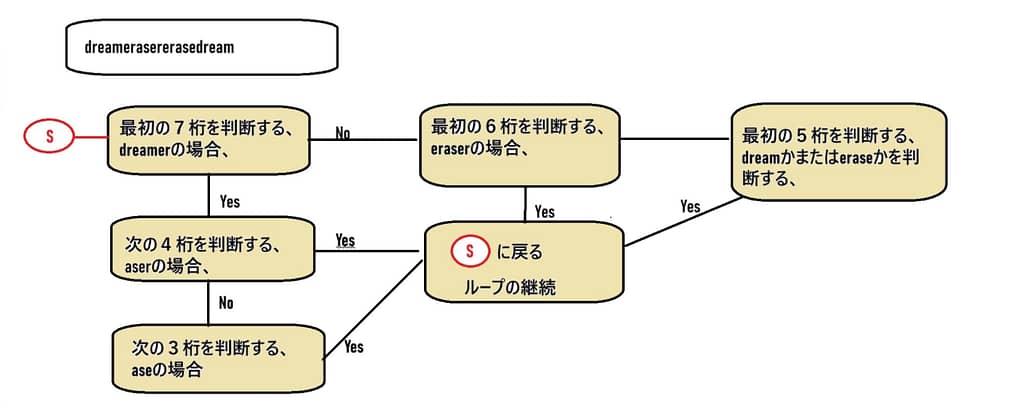
この方法は正解にたどり着くけど、ちょっと面倒くさいと思います。
後編、動的計画法を用いて、この問題の解き方について、述べたいと思います。