—2025/04/17
連日の晴れ、4月並みの暖かさを感じて、ぽかぽか…
今日、Atcoder094回目を挑戦しようと思います。
まずC問題を着目します。
N個の数X₁、X₂、…、Xnを与えて、Nは偶数で、i=1,2,…nに対して、X₁、X₂、…、XnからXiのみを除いたもの、X₁、X₂、…,Xi−1,Xi+1,…Xnの中央値を求める問題。
中央値を求める問題ですね、予備知識としては、k個数字(kは奇数)の中央値は(k+1)/2番目大きい数値であること。
よくわからないですが、具体例を見てみる、
4つの数字2,4,4,3に、それぞれの数字を除いて、その中央値は、
①2を除いて、4,4,3の中央値は2番目大きい数値4です。
②4を除いて、2,4,3の中央値は2番目大きい数値3です。
③4を除いて、2,4,3の中央値は2番目大きい数値3です。
④3を除いて、2,4,4の中央値は2番目大きい数値4です。
以上の流れを考察すると、気付いた箇所があります。Nは固定なので、一つ数字を取り除くと、結果は必ずN/2番目大きい数値、因みに取り除かれた数字はそれより小さいであれば、N/2番目大きい数値に影響を与えないので、N/2番目大きい数値は正解です、取り除かれた数字値それより大きいまたはそれと同じであれば、どうなっているのか?大きい順は一つずらされ、N/2 -1番目大きい数値は正解になりますね。
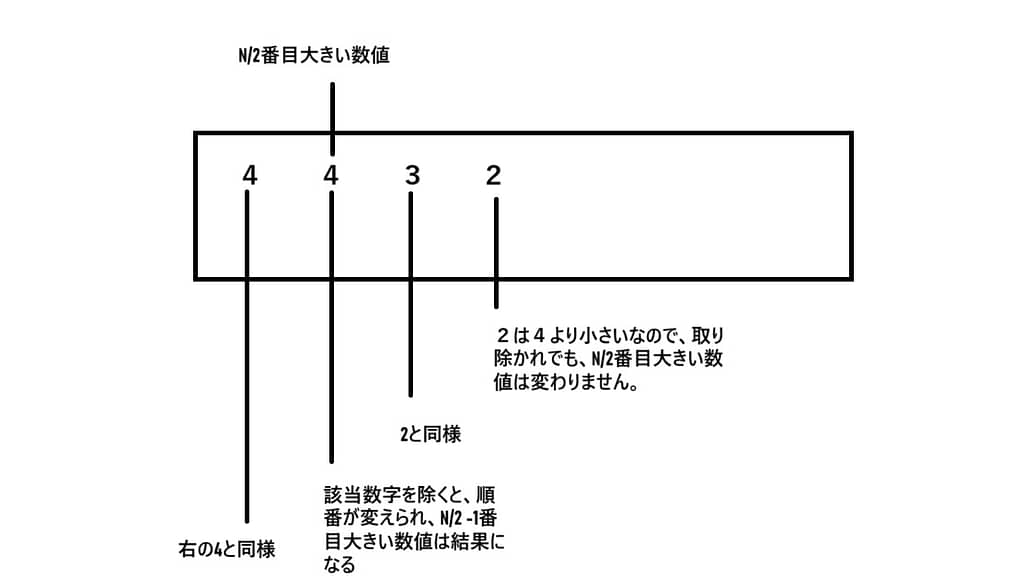
このように考えて、実装はかなり楽になり、計算量はO(N)です。
実装する際、ソート前後の番号を記録できるようなテクニックを駆使しました。
今日ここまでにします。
crossorigin="anonymous">