
——————動的計画法
動的計画法はアルゴリズムの中にとても重要のひとつ、ネット上にもいろんな紹介サイトがあるが、ちょっと検索したら、以下のような
うさぎでもわかるアルゴリズム 動的計画法 等々 出ている。
でも、動的計画法は万能ではなく、ループ処理の回数は50以下なら、問題がなさそうだが、
50より大きくなると、処理自体タイムオーバーになると思う。
今回Atcoder 044回目を挑戦した。その中のC問題が動的計画法を用いて、実装することになった。
概ね、N枚のカードから数枚選んで、そのカードに書かれた数字の平均値はAになる通り数を求めること。
例えば、
4枚カードにそれぞれ以下の数字が書かれた、7、9、8、9
その中からいくつを選んで、平均値は8となる通り数を求める。
平均が8 となるカードの選び方は、以下の
5 通りだ。
3 枚目のカードのみを選ぶ。
1 枚目と2 枚目のカードを選ぶ。
1 枚目と4 枚目のカードを選ぶ。
1 枚目と2枚目および3 枚目のカードを選ぶ。
1 枚目と3枚目および4 枚目のカードを選ぶ。
一見数学の確率問題が、Nは50以下なので、典型的な動的計画法DP問題だ。
考案として、
①3次元の配列を作成する、dp[x][y][z]、x—>何枚目のことを指す、y—>選んだ枚数、z—>選んだカードの総和
②x毎に判断する時、このカードを選ぶか選ばないか2通りがあるので、それぞれ考慮して、配列を作成すること
③選んだカードの平均値はAであることは、つまり選んだカードの総和はA*yということになる。(yは枚数)
以上を元に、実装したソースは
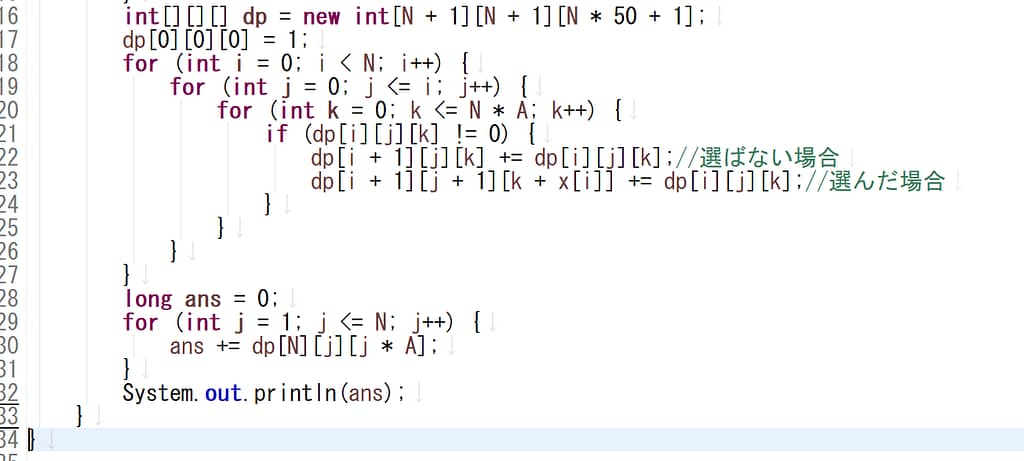
このように実装した結果、正解にたどり着いだ。