—2025/04/23 動的計画法②——————-後編
連日の晴れにピリオド、今日はしくしく雨でした。
前編「Javaばば挑戦中⑨ – Javaばばの部屋」の続き、今日は同じ問題に、動的計画法を用いて、どのように考えたかを書きたいと思います。
問題
英小文字からなる文字列 S が与えられます。 Tが空文字列である状態から始め、以下の操作を好きな回数繰り返すことで S=Tとすることができるか判定してください。
文字列 Sの最大長さは10⁵になる。
- T の末尾に
dreamdreamereraseeraserのいずれかを追加する。
例えば、
このような文字列Sは dreamerasererasedream 、TをSと同じ文字列に作れるか?
考え方、
配列dp[N]を用意して、文字列 Sの最長は10⁵なので、N=100000
dp[0]~dp[100000]までに、読み込まれた文字列 Sに対して、以下のように判別し、結果はYesの場合に
dp[ ] を1にセット、結果はNoの場合に、dp[ ] を0にセットする。
判別方法:
①指針index = 0, dp[0] = 1 にセット、スタート点は文字列の最初からです。dp[index] = 1の前提で、②~④までループ処理を行う
②文字列Sのindex番目からindex+5番目までは”erase”或”dream”であれば、dp[index+5] = 1をセットする、erase或dreamが見つかったという意味している
③文字列Sのindex番目からindex+6番目までは”eraser”であれば、dp[index+6] = 1をセットする、eraserが見つかったという意味している
④文字列Sのindex番目からindex+7番目までは”dreamer”であれば、dp[index+7] = 1をセットする、dreamerが見つかったという意味している
⑤指針index+1、文字列Sの次の文字に対象して、②~④のループ処理が続く、文字列Sの最後まで
⑥ループ処理が終了後、dp[S.文字列長さ] = 1 、つまり、文字列Sの最初文字から最後文字まで全て見つかったという意味している、この場合、文字列Sが存在する、それ以外、文字列Sが存在しない。
流れ図は、
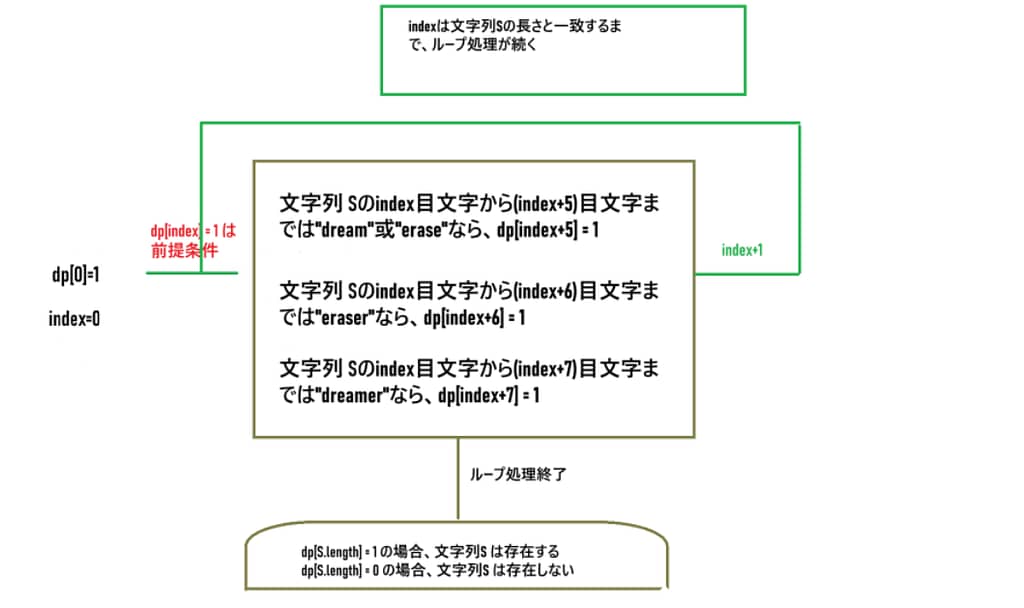
前述の例を参考に、実行したら、以下の結果になります、

この問題は動的計画法を巧みに利用して、効率的に解くことができました。
動的計画法が機械的に、あらゆる組み合わせの可能性を数値の形に保存し、実装することも楽くなりますね、Javaばばはそういう問題の解くスキルはまだまだ未熟で、今後もっと解きたいと思います。