—2025/05/01
今日曇り所により晴れです。季節の変わり目で、冬服や、冬布団の片付けが日々少しずつやっています、服を捨てると幸せが見つかるという噂話を聞いたことありますが、服を捨てられない私は断捨離意識が低いですね。
さておき、やっぱりAtcoder問題にいきましょう。
問題
N 人の人が東西方向に一列に並んでいます。 それぞれの人は、東または西を向いています。 誰がどの方向を向いているかは長さ Nの文字列 S によって与えられます。 西から i 番目に並んでいる人は、Si= E なら東を、Si= W なら西を向いています。
あなたは、N人のうち誰か 1 人をリーダーとして任命します。 そして、リーダー以外の全員に、リーダーの方向を向くように命令します。 このとき、リーダーはどちらの方向を向いていても構いません。
並んでいる人は、向く方向を変えるのを嫌っています。 そのためあなたは、向く方向を変える人数が最小になるようにリーダーを選びたいです。 向く方向を変える人数の最小値を求めてください。
小さい頃体育の授業で、班長はリーダーで、みんな一列並んで、一斉に班長の方向に向いていることよく経験したことがあります。今回の問題は、リーダーは一番前の班長とは限りません、誰を選んで、皆の方向回転回数が最も少なくさせる人はリーダーになります。
分かりやすく説明するために、例を挙げます。
五人の人が一列WEEWWに並んで、つまり「西東東西西」です。
図を見てください。
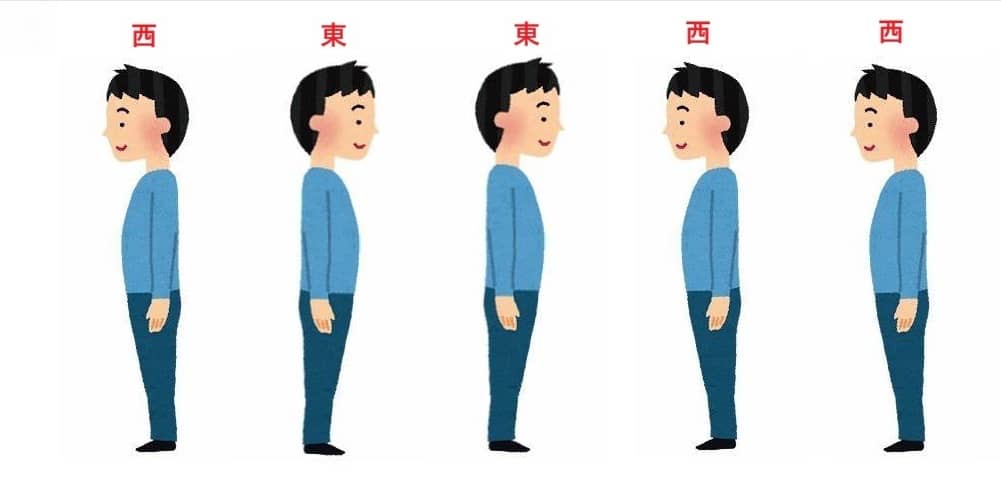
この類の問題について、私は前の投稿にも言及したことがありますが、最小値や最大値の問題なので、すべての可能性を考慮する必要があります、典型的な全探索問題です、全探索問題の処理時間の見積もりをまず考えます。人数の最大値は10⁵なので、最大O(N)に収める必要があると思います、つまりループ処理は2重にしたら、O(N²)になると時間オーバーになります。
では、全探索の思考回路に沿って、操作していきましょう。
まず、1人目の人がリーダーとして、皆の向き変える回数を見てみる、
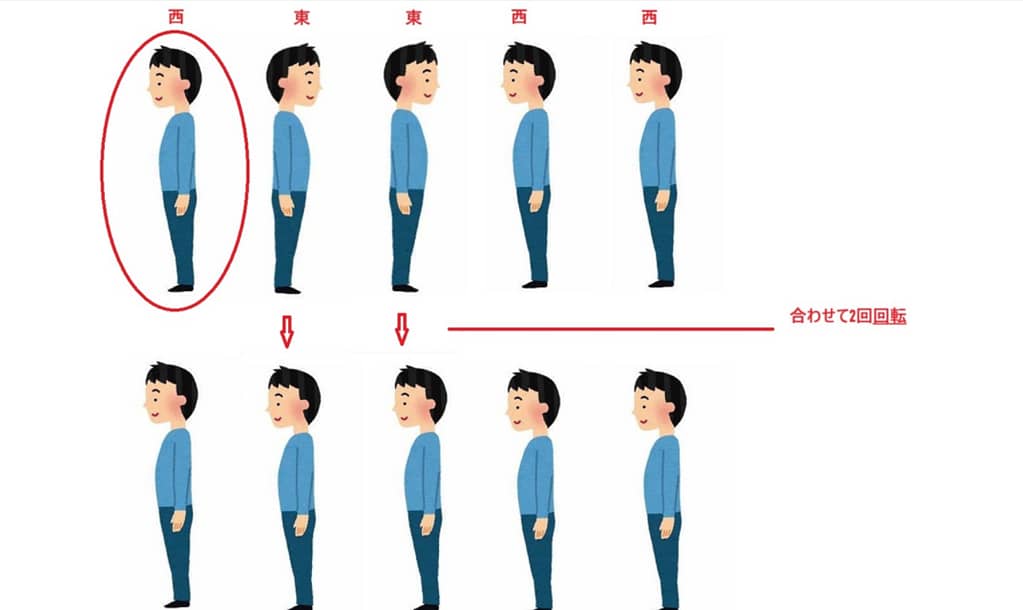
1人目の人がリーダーになったら、合わせて皆の回転回数は2回です。
次、2人目の人がリーダーになったら、どうでしょうか?
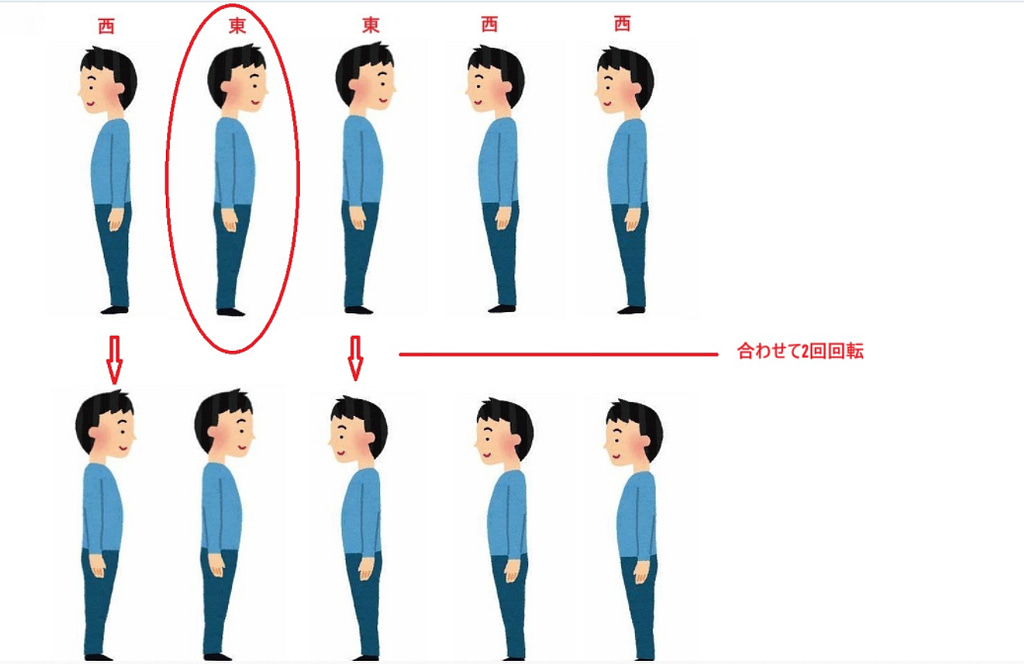
2人目の人がリーダーになったら、合わせて皆の回転回数は2回です。
次、3人目の人だったら、
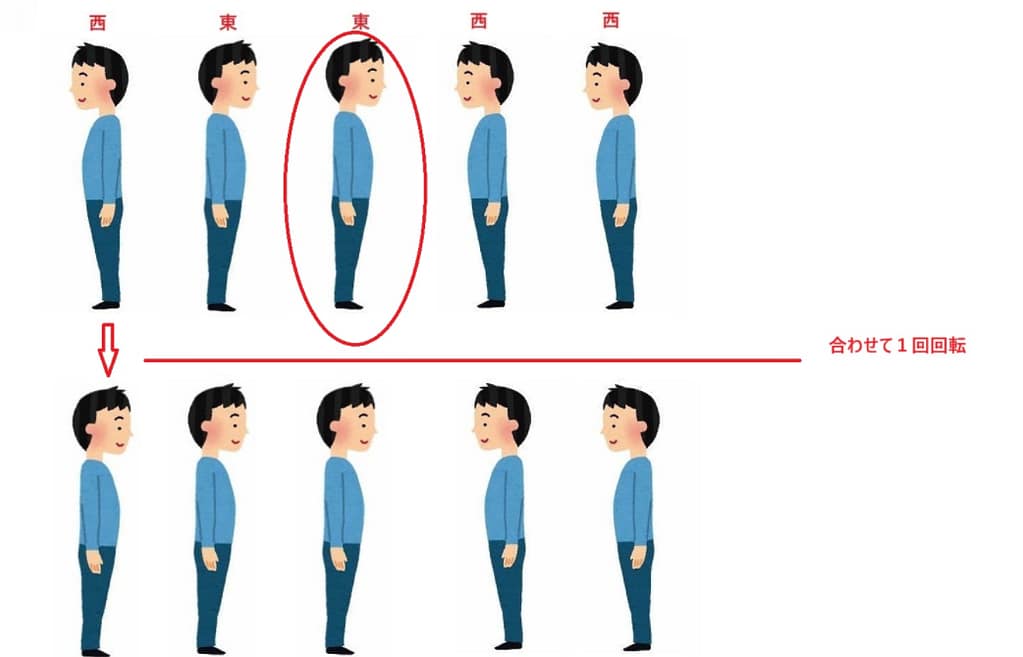
3人目の人がリーダーになったら、合わせて皆の回転回数は1回です。
次、4人目だったら、
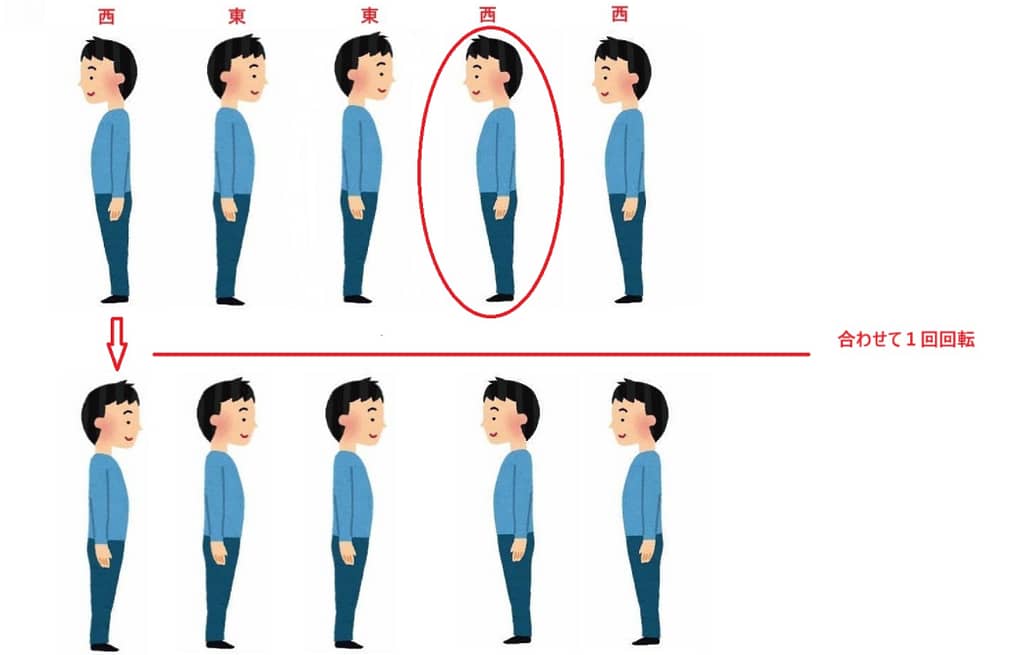
4人目の人がリーダーになったら、合わせて皆の回転回数は1回です,3人目リーダーの結果と同じです。
次、5人目だったら、
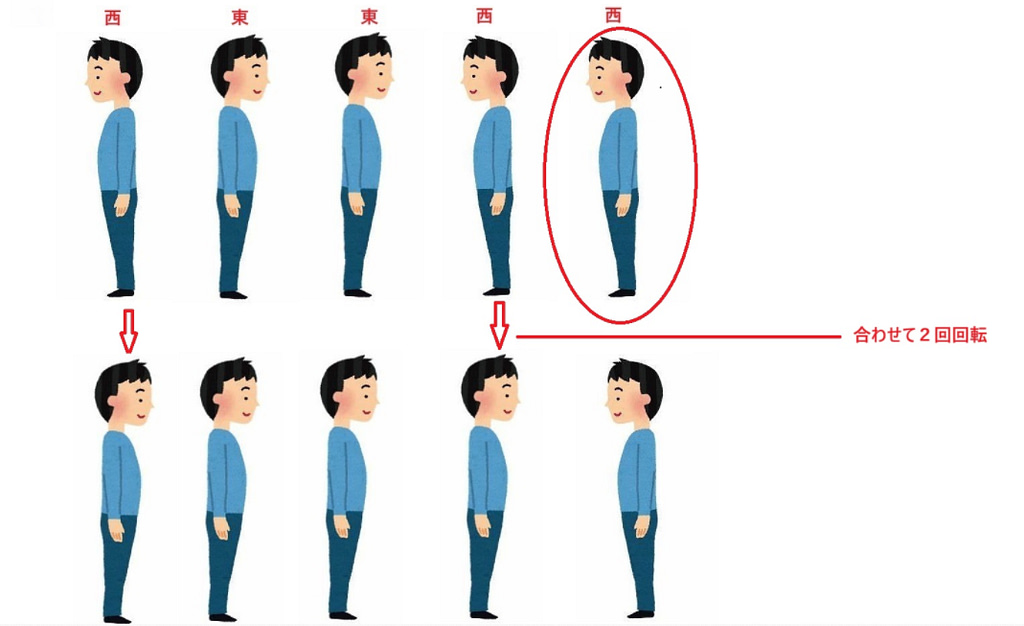
5人目の人がリーダーになったら、合わせて皆の回転回数は2回です。
以上の結果によって、3人目或4人目をリーダーになったら、最小回転回数は1回です。
しかし、これだけの流れで、どんなヒントが得られますか?
つまり、例を見て、解決方法をまとめましょう。
後編に纏めたヒントを説明したいと思います。
では、引き続き、明日のブログをお楽しみに。